HTML5 CanvasのarcToをarcで実装してみた
はじめに
前回のエントリ「HTML5 Canvas のarcTo関数の実装が未だにorz」で書いたCanvasのarcToですが、これをarcで実装してみました。CanvasのarcTo関数は左図のように3点A, B, Cが与えられたとき、その2本の半直線に接する半径Rの円弧を描画するものです。
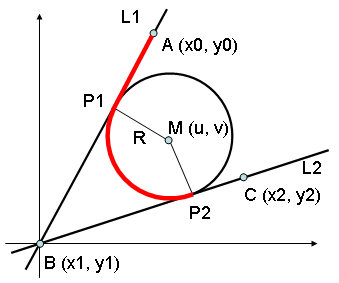
結果のJavaScriptプログラムは非常にシンプルになりましたが、そこに到るステップはちょっと面倒でした。今回のエントリーは高校の数学の復習的な内容になっています。昔を思い出して紙と鉛筆だけの手計算をしました。
2本の直線に接する円を求める
arcToを実装するポイントは下記の問題を解くことです。
平行ではない2本の直線に接する半径Rの円の中心と2つの接点の座標を求めよ。
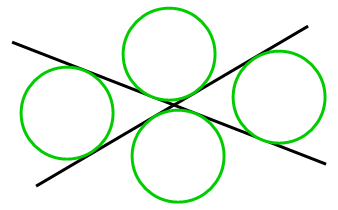
2本の直線に接する円は左図のように4つ存在します。ここでは途中の計算を簡単にするため、2の直線は原点を通り傾きが無限大でないものとします。つまり、2本の直線は下記のように表されます。
(1) L1: y=m1x
(2) L2: y=m2x
原点を通らない直線は単純な平行移動なので、最後の結果をシフトすればよいだけです。
直線に接する円の中心は、直線からの距離がRということから、最初に直線と点との距離を計算しておきます。
直線y=mx と点 (u, v)の距離を求めよ。
距離と同時に点から直線に下ろした垂線の足の座標も円との接点として必要なので、ここでは、直線をパラメータ表現して点(u, v)との距離が最短になる点を求めます。直線上の点はパラメータをtとしたとき(t, mt)なので、点(u, v)との距離をdとすると、
d2=(t−u)2+(mt−v)2
\hspace{18} = (1 + m^2)t^2 - 2(u + mv)t + u^2 + v^2
となります。このd2が最小になるtの値を求めればよいので、答えは中学生でも出せますが、ここでは面倒なので微分してゼロとなるときのtの値を計算すると、
(3) t=u+mv1+m2
のとき、d2が最小になり、そのときのd2の値は
(4) d2=(v−mu)21+m2
になります。
さて、本題に戻ります。原点を通る直線L1とL2上の点をパラメータ表現してそれぞれ(t1, m1t1), (t2, m2t2)とし、これをベクトルとしたとき、円の中心座標Mはこの2つのベクトルの合成であるから、
(5) 円の中心座標 M: (t_1 + t_2, \hspace{14} m_1 t_1 + m_2 t_2)
と表されます。この点Mと直線L1, L2との距離がRであるということから、
R2=(m1t1+m2t2−m1(t1+t2))21+m21
R2=(m1t1+m2t2−m2(t1+t2))21+m22
すなわち、
(6) R2=(m2−m1)2t221+m21
(7) R2=(m2−m1)2t211+m22
が成立します。
t1, t2について解くと、
(8) t1=±R√1+m22|m2−m1|
(9) t2=±R√1+m21|m2−m1|
になります。このt1, t2を(5)に代入した4点が2直線に接する半径Rの円の中心座標ということになります。
また、そのときの接点の座標は(t, mt)であり、tは(3)であるから、
(10) (t_1 + t_2\frac{1 + m_1 m_2}{1+m_1^2}, \hspace{12} (t_1 + t_2\frac{1 + m_1 m_2}{1+m_1^2})m_1)
(11) (t_2 + t_1\frac{1 + m_1 m_2}{1+m_2^2}, \hspace{12} (t_2 + t_1\frac{1 + m_1 m_2}{1+m_2^2})m_2)
となります。
任意の2直線に一般化する
次に、直線の傾きmが無限大のとき(つまりx=a)も考慮して、原点を通る全ての直線のときに一般化します。原点を通る直線は
ax+by=0
ですから、(1),(2)の式にそれぞれ m1=−b1/a1, m2=−b2/a2 を代入して、式を整理してa1, a2が分母にならないようにします。結果だけを書きます。
下記の2直線
a1x+b1y=0
a2x+b2y=0
に接する半径Rの円の中心Mは
M: (k_1 b_2 + k_2 b_1, \hspace{14} -(k_1 a_2 + k_2 b_1) )
ただし、
k1=±R√a21+b21|a1b2−b1a2|
k2=±R√a22+b22|a1b2−b1a2|
また、そのときの接点の座標は、
(b_1(k_2 + j_1), \hspace{14} -a_1(k_2 + j_1) )
(b_2(k_1 + j_2), \hspace{14} -a_2(k_1 + j_2) )
ただし、
j1=k1a1a2+b1b2a21+b21
j2=k2a1a2+b1b2a22+b22
求めるものはこの4つの円のうちの1つですが、傾きのmをベクトルとして計算したので、m = -b/a を考慮して、k1とk2の符号が負のものが求める円の中心と接点ということになります。
描画する円弧を求める
さて、以上で円の中心と2つの接点の座標が求まりました。次に、接点を結ぶ2つの円弧のうちどちらの円弧を描画すればよいかを計算します。
arc関数では円弧の描画は円中心からの2つの角度と時計回りか半時計回りかを指定します。そこで、この2つの角度と円弧の描画方向を円の中心の座標と2つの接点の座標から計算します。
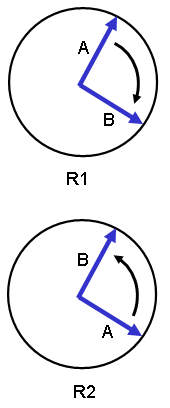
arcToの仕様では点(x1, y1)に近いほうの円弧を描画すると書かれています。これは短い方の円弧ということになりますが、AとBの角度が必ず鋭角になるということであり、R1かR2かを区別すればよいことになります。
これにはベクトルA, Bの外積を計算すればその方向が逆になるので判別できます。外積といっても、z値がゼロなので式は単純です。(a, b, 0), (c, d, 0)の外積は(0, 0, ad-bc)になります。
つまり、図でAとBの外積A×Bのz成分が正なら半時計まわりです。この通り、円の中心から接点へのベクトルを求めてもよいのですが、単なる符号が必要なだけなので、最初の図で交点Bを基点としたBAとBCのベクトルの外積のz成分を求め符号を反転したものと同じになります。
(x0-x1)*(y2-y1) > (y0-y1)*(x2-x1) なら反時計周り、そうでなければ時計回りに円弧を描画すればよいことになります。
プログラムコード
以上を整理してJavaScriptで実装すると下記のようになります。Canvas APIのarcToとの違いは、パス中の現在の座標(x0, y0)を明示的に引数に指定している点です。3点A, B, Cが一直線上にあるときは変数mmがゼロになるときです。さらに、この条件はA=BあるいはB=Cのときも含みます。OperaとFirefoxでは長さゼロの線分はlineCapがroundやsquareのときも何も描画されないので、0.1だけ長くするというワークアラウンドを入れています。
さらに、符号を整理して不要な負の符号が出現しないようにa1, a2を反転させています。
function arcTo(path, x0, y0, x1, y1, x2, y2, rad) { var a1 = y0 - y1; var b1 = x0 - x1; var a2 = y2 - y1; var b2 = x2 - x1; var mm = Math.abs(a1*b2 - b1*a2); if (mm === 0 || rad === 0) { if (a1 === 0 && b1 === 0 && path.lineCap !== "butt") { // Workaround for Opera and Firefox. path.lineTo(x1, y1 + 0.1); } else { path.lineTo(x1, y1); } } else { var dd = a1 * a1 + b1 * b1; var cc = a2 * a2 + b2 * b2; var tt = a1 * a2 + b1 * b2; var k1 = rad * Math.sqrt(dd) / mm; var k2 = rad * Math.sqrt(cc) / mm; var j1 = k1 * tt / dd; var j2 = k2 * tt / cc; var cx = k1 * b2 + k2 * b1; var cy = k1 * a2 + k2 * a1; var px = b1 * (k2 + j1); var py = a1 * (k2 + j1); var qx = b2 * (k1 + j2); var qy = a2 * (k1 + j2); var ang1 = Math.atan2(py - cy, px - cx); var ang2 = Math.atan2(qy - cy, qx - cx); path.lineTo(px + x1, py + y1); path.arc(cx + x1, cy + y1, rad, ang1, ang2, b1 * a2 > b2 * a1); } }
テストケース
前回作ったテストケースをこのarcTo()関数で実行させてみました。
| Firefox | Chrome | Safari | Opera | IE |
|---|---|---|---|---|
| 3.6 | 5.0.307.1 dev | 4.04 | 10.10 | 8.0 + excanvas-r3 |
実際の動作は以下よりアクセスできます。
顔の部分をクリックすると、オリジナルのarcTo関数を使った場合の描画がトグルで切り替わります。ここで書いた自前のarcTo関数の結果、ChromeとSafariでは期待される結果となりました。

Firefoxは最近リリースされたVer3.6でarcTo()の実装が改善されています。しかし、A, B, Cが直線上にありscale変換を伴うとき問題があるようです。左図はVer3.6のarcTo関数で描画したものです。

一方、左図はここで書いたarcToをOperaで実行したときの結果です。右の口が裂けていて、左の眉毛も剃られています。なぜこうなるのか?これは、lineJoinの実装の方法の違いのように思われます。IEのExCanvasにも同様のものが観測されました。機会があれば、別のエントリーで書きたいと思います。